Der Begriff Potential wurde schon mit dem Gravitationsfeld eingeführt. Hier hat jeder Massepunkt in jedem Raumpunkt eine bestimmte potentielle Energie. In diesem Zusammenhang verstehen wir, dass wir zum Heben einer Masse vom tiefer liegenden Punkt A,  auf ein um s höher liegendes Niveau im Punkt B, Arbeit verrichten müssen. Diese ist gleich der Kraft F multipliziert mit dem Weg s. Die potentielle Energie bekommen wir in Form kinetischer Energie wieder zurück, wenn die Masse herunterfällt. Wollen wir den Arbeitsaufwand und damit die Energie welche wir zurückbekommen wissen, macht es macht nur Sinn, wenn wir die Potentialdifferenz zwischen den Punkten A und B wissen. Das Bestimmen eines beliebigen Nullpunktes hat mitunter praktische Bedeutung. Für die physikalischen Gesetzmäßigkeiten kommen jedoch immer nur Potentialdifferenzen in Betracht.

Wir können den Raum um eine elektrische Ladung mit dem elektrischen Feld, aber auch durch das elektrische Potential in den einzelnen Raumpunkten beschreiben.  Das elektrische Potential in einem Raumpunkt ist definiert, als die potentielle Energie, die ein mit der positiven Ladungseinheit geladener Massepunkt infolge seiner Anwesenheit an jener Stelle des Raumes im Einflussbereich der Ladung besitzt. Nicht immer ist die präzise Darstellung des Feldes durch ein Vektorfeld (Kraftfeld) erforderlich.  Wenn nicht nach den Kräften, sondern nach den Energiezuständen gefragt ist, genügt die Darstellung mittels des skalaren Potentialfeldes.

Das elektrische Potential φ in einem Raumpunkt P ist definiert als die potentielle Energie, die eine mit positiver Ladungseinheit geladene Probeladung Q⁺ besitzt um sie an diesen Raumpunkt zu bringen.

Beispiel: An einem Punkt P im Raum eines ruhenden elektrischen Feldes wird das elektrische Potential φ_(P) gemessen.

Am Ort P₁ des elektrischen Feldes besteht das Potential φ₁, an der Stelle P₂ das Potential φ₂.

Es wurde φ₂ größer als φ₁ bestimmt.

Die Energie W₂₁ die an der Probeladung Q⁺ am Weg s von P₁ zu P₂ aufgewendet werden muss beträgt: W₂₁ =  W₂ – W₁ = F·s. Um eine Feldgröße zu gewinnen welche unabhängig vom Betrag der Probeladung ist, bilden wir den Quotienten φ = W / Q⁺.
Für W₂₁ erhalten wir dann W₂₁ = W₂ – W₁ = Q⁺·φ₂ – Q⁺·φ₁ = Q⁺ (φ₂ – φ₁).

Um die positive Probeladung Q⁺ in einem elektrischen Feld vom Ort P₁ mit dem Potential φ₁, zum Ort P₂ mit dem Potential φ₂ zu bringen, muss die Arbeit W₂₁ = Q⁺ ·(φ₂– φ₁)   aufgewendet werden.

Diese Arbeit hängt nur von der Potentialdifferenz ab und ist unabhängig vom Weg und von der Wahl eines Bezugspunktes.

Die Einheit des elektrischen Potentials ergibt sich als Quotient aus der Arbeitseinheit Joule und der Ladungseinheit Coulomb.  1J / 1C = 1V.

Der Potentialunterschied zwischen φ₂ und φ₁ ist die elektrische Spannung U. Die abgeleitete Einheit des elektrischen Potentials ist das Volt.

Potentialunterschied, Spannung

Höheres Potential

Niederes Potential

V

V

V

U₂₁ = φ₂ ─ φ₁

Die Spannung wirkt vom höheren Potential zum niederen Potential. Verläuft ein Spannungspfeil vom höheren zum niederen Potential hat die Spannung einen positiven Betrag. Wird der Spannungspfeil vom niederen zum höheren Potential gezeichnet, erhält der Spannungswert einen negativen Betrag.

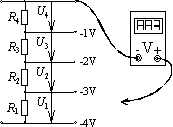
Der Potentialbegriff wird auch auf die elektronischen Schaltungen angewendet. Es wird jedem Punkt in der Schaltung ein Potential zugemessen. Für eine Potentialmessung wird ein Spannungsmesser verwendet. Das Vorzeichen in der Anzeige des Messwerts liefert die Aussage, ob das Potential gegenüber dem Bezugsniveau (Bezugspunkt) positiv oder negativ ist.

Je nach Wahl des Bezugspunktes können die Messwerte an den Messpunkten positive oder negative Werte haben.